CS/Computer Graphics
어파인 공간(Affine Space), 동차좌표(Homogeneous coordinates)
테크 로그포스
2023. 4. 25. 15:12
1. 어파인 공간
벡터는 크기와 방향을 포함하는데, 정점요소는 없다.
그러므로 점과 벡터를 동족취급하여 벡터공간을 확장한 공간이 어파인 공간이다.
1-2. 어파인 연산
어파인 공간의 어파인 연산에서는
- 벡터와 벡터의 덧셈뺄셈
- 스칼라와 벡터의 곱셈나눗셈은 물론
- 점과 벡터의 덧셈 및 뺄셈이 가능해진다.
이에 따라 어떤 점을 표시할 수 있고 선분을 표시할 수 있다.
점과 점의 덧셈/뺄셈은 계수 합이 1일 때만 허용된다. (어파인 합(Affine Sum))
2. 동차좌표
공간에서 벡터와 점은 표현 방식이 다르다. (v=4V1+2V2+V3, P=r+4V1+2V2+V3)
점과 벡터를 동일한 방식으로 표현하기 위해서 동차좌표를 정의하는 것이다.
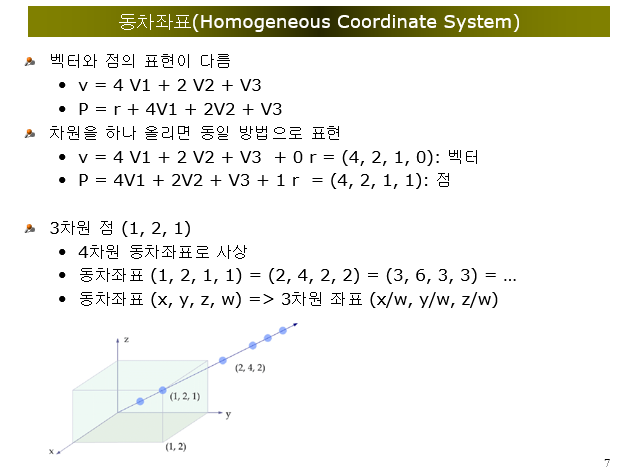
예를 들면, 3차원 좌표를 3개의 요소로 표현하는 게 아니라
한 차원 올려서 4개의 요소로 통일되게 표현한다. (2차원의 경우 3개의 요소로 표현하는 것)
이를 통해 점과 벡터를 동일한 방법으로 표현 가능해지며,
마지막 요소가 0이면 벡터, 1이면 점을 의미하는 것으로 해석할 수 있다.
cf) 컴퓨터 그래픽에서는 모든 좌표를 동차 좌표로 표시한다.
3차원 그래픽 파이프라인 하드웨어는 동차 좌표 처리를 위해 한 번에 4개의 요소로 입력하고 처리할 수 있도록 설계되어있다고 한다.